Minimax criterion: Difference between revisions
m (→Application) |
m (Text cleaning) |
||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
Min-max criterion - is a decision-making criterion presented in 1954 by Leonard Savage. This criterion minimizes the expected loss associated with making worse than optimal decision, for a given state of nature. In the decision-making [[process]] such [[strategy]] should be selected, for which the relative loss is the smallest. | Min-max criterion - is a decision-making criterion presented in 1954 by Leonard Savage. This criterion minimizes the expected loss associated with making worse than optimal decision, for a given state of nature. In the decision-making [[process]] such [[strategy]] should be selected, for which the relative loss is the smallest. | ||
| Line 107: | Line 92: | ||
Summing up: | Summing up: | ||
According to the Min-max manager should choose a strategy '''T3'''. | According to the Min-max manager should choose a strategy '''T3'''. | ||
==Advantages of Minimax criterion== | |||
The Minimax criterion has several advantages in decision-making. These include: | |||
* It helps to minimize the [[risk]] of making a wrong decision, as it helps to identify the best possible solution in the given state of nature. | |||
* It is simple and easy to understand and apply. | |||
* It is based on the concept of maximizing the minimum gain, which ensures that all possible outcomes are taken into account. | |||
* It is a robust decision-making criterion, as it is not affected by changes in the [[environment]] or the circumstances. | |||
* It is a cost-effective approach, as it does not require any additional resources to be used. | |||
==Limitations of Minimax criterion== | |||
The Minimax criterion has several limitations: | |||
* It assumes that all outcomes are known, which is rarely the case in real-world scenarios. Additionally, it ignores the uncertainty of the outcomes, which can make it difficult to accurately evaluate the risks associated with different decisions. | |||
* It only considers the worst-case scenario when evaluating the expected loss of different [[options]], and does not consider other scenarios which might be more beneficial. | |||
* It does not take into account the preferences or values of the [[decision-maker]], which can lead to suboptimal decisions. | |||
* It can be computationally complex, making it difficult to use in practice. | |||
==Other approaches related to Minimax criterion== | |||
Here is a list of other approaches related to Minimax criterion: | |||
* Maximin criterion - it is a decision-making criterion which is based on maximizing the expected minimum gain associated with making an optimal decision, for a given state of nature. | |||
* Hurwitz criterion - it is a decision-making criterion which takes into account both the expected gain and the expected loss. It is based on minimizing the maximum expected loss associated with making a sub-optimal decision, for a given state of nature. | |||
* Bayes criterion - it is a decision-making criterion which takes into account the prior probabilities when making decisions. It is based on minimizing the expected risk associated with making a sub-optimal decision, for a given state of nature. | |||
* Laplace criterion - it is a decision-making criterion which takes into account the prior probabilities as well as the expected gain and loss when making decisions. It is based on minimizing the expected risk associated with making a sub-optimal decision, for a given state of nature. | |||
In summary, other approaches related to Minimax criterion are Maximin criterion, Hurwitz criterion, Bayes criterion, and Laplace criterion. Each of these approaches is based on minimizing the expected loss associated with making worse than optimal decisions, for a given state of nature. | |||
{{infobox5|list1={{i5link|a=[[Maximin criterion]]}} — {{i5link|a=[[Expected utility theory]]}} — {{i5link|a=[[Conditions of decision-making]]}} — {{i5link|a=[[Decision process models]]}} — {{i5link|a=[[Expected utility]]}} — {{i5link|a=[[Quantitative risk analysis]]}} — {{i5link|a=[[Selection process in conditions of certainty and uncertainty]]}} — {{i5link|a=[[Influence diagram]]}} — {{i5link|a=[[Analysis of preferences]]}} }} | |||
==References== | ==References== | ||
* Bierwag, G. O., & Khang, C. (1979). ''[http://onlinelibrary.wiley.com/doi/10.1111/j.1540-6261.1979.tb02101.x/full An immunization strategy is a minimax strategy]''. The Journal of Finance, 34(2), 389-399. | * Bierwag, G. O., & Khang, C. (1979). ''[http://onlinelibrary.wiley.com/doi/10.1111/j.1540-6261.1979.tb02101.x/full An immunization strategy is a minimax strategy]''. The Journal of Finance, 34(2), 389-399. | ||
[[Category:Decision making]] | [[Category:Decision making]] | ||
[[pl:Kryterium minimaksowe]] | [[pl:Kryterium minimaksowe]] | ||
Latest revision as of 00:51, 18 November 2023
Min-max criterion - is a decision-making criterion presented in 1954 by Leonard Savage. This criterion minimizes the expected loss associated with making worse than optimal decision, for a given state of nature. In the decision-making process such strategy should be selected, for which the relative loss is the smallest.
Application
According to the criterion you must first find a matrix of relative loss (a matrix of grief). Loss is defined as the difference between the greatest win, for a particular state of nature, and winning that corresponds to the predicted results of current decision. The calculations are made in columns in each of them going to the largest value, and then typed in the array of grief, the difference between the highest value and the currently calculated. This process can be expressed in following equation:
The next step is, specifying maximum loss for each strategy, and at the end selection of the strategy for which the maximum loss, will be the largest. Model:
Example
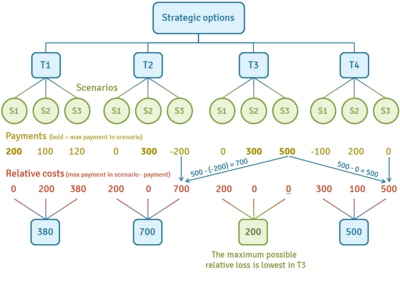
Example: we have an array of payments from the four possible decisions and three possible states:
| I | II | III | |
| T1 | 200 | 100 | 120 |
| T2 | 0 | 300 | −200 |
| T3 | 0 | 300 | 500 |
| T4 | −100 | 200 | 0 |
On this basis cost matrix of relative loss is calculated. Each value in column is subtracted from max values in scenario I/II/III:
| I | II | III | |
| T1 | 0 | 200 | 380 |
| T2 | 200 | 0 | 700 |
| T3 | 200 | 0 | 0 |
| T4 | 300 | 100 | 500 |
We are looking for the maximum losses for each strategy, and then select the smallest:
| Strategies | |
| T1 | 380 |
| T2 | 700 |
| T3 | 200 |
| T4 | 500 |
Summing up: According to the Min-max manager should choose a strategy T3.
Advantages of Minimax criterion
The Minimax criterion has several advantages in decision-making. These include:
- It helps to minimize the risk of making a wrong decision, as it helps to identify the best possible solution in the given state of nature.
- It is simple and easy to understand and apply.
- It is based on the concept of maximizing the minimum gain, which ensures that all possible outcomes are taken into account.
- It is a robust decision-making criterion, as it is not affected by changes in the environment or the circumstances.
- It is a cost-effective approach, as it does not require any additional resources to be used.
Limitations of Minimax criterion
The Minimax criterion has several limitations:
- It assumes that all outcomes are known, which is rarely the case in real-world scenarios. Additionally, it ignores the uncertainty of the outcomes, which can make it difficult to accurately evaluate the risks associated with different decisions.
- It only considers the worst-case scenario when evaluating the expected loss of different options, and does not consider other scenarios which might be more beneficial.
- It does not take into account the preferences or values of the decision-maker, which can lead to suboptimal decisions.
- It can be computationally complex, making it difficult to use in practice.
Here is a list of other approaches related to Minimax criterion:
- Maximin criterion - it is a decision-making criterion which is based on maximizing the expected minimum gain associated with making an optimal decision, for a given state of nature.
- Hurwitz criterion - it is a decision-making criterion which takes into account both the expected gain and the expected loss. It is based on minimizing the maximum expected loss associated with making a sub-optimal decision, for a given state of nature.
- Bayes criterion - it is a decision-making criterion which takes into account the prior probabilities when making decisions. It is based on minimizing the expected risk associated with making a sub-optimal decision, for a given state of nature.
- Laplace criterion - it is a decision-making criterion which takes into account the prior probabilities as well as the expected gain and loss when making decisions. It is based on minimizing the expected risk associated with making a sub-optimal decision, for a given state of nature.
In summary, other approaches related to Minimax criterion are Maximin criterion, Hurwitz criterion, Bayes criterion, and Laplace criterion. Each of these approaches is based on minimizing the expected loss associated with making worse than optimal decisions, for a given state of nature.
| Minimax criterion — recommended articles |
| Maximin criterion — Expected utility theory — Conditions of decision-making — Decision process models — Expected utility — Quantitative risk analysis — Selection process in conditions of certainty and uncertainty — Influence diagram — Analysis of preferences |
References
- Bierwag, G. O., & Khang, C. (1979). An immunization strategy is a minimax strategy. The Journal of Finance, 34(2), 389-399.