Adjusted mean

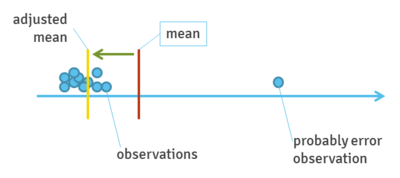
Adjusted mean - term used in statistics, in statistical analysis. Otherwise called least-squares mean.

Is a mean adjusted for certain data that could lead to misinterpretation. If in the data, far from center there are some values, the mean won't work properly . Adjusted mean is often used in an ANCOVA (Analysis of Covariance) .

Adjusted mean usage

For example, try to calculate mean from values: 2, 3, 3, 4, 3, 4, 5, 2, 130. The last value will move average significantly. Mathematically it is correct, but in real life it is probable that 130 is an error or one-time value. Adjusted mean, known also as least-squares mean lets remove such outliers and present .

Mean is a measure that can be easily manipulated and thus misinterpreted. It should always be used together with :

• standard deviation,
• and other statistical measures.

Fig.1. Adjusted mean example

Adjusted mean interpretation

An adjusted mean determines an expected result. To precise, it is the predicted mean dependent variable score for studied group of subjects in the situation, when the covariate mean has exactly the same value as the grand covariate mean. The various samples from studies, even when using the method of random sampling, usually cannot provide exactly the same value of covariate mean. Because of that and the fact that covariate is highly related to the dependent variable, the head researcher may consider the reason of that. For example, this situation may be caused by some differences between studied groups. By computing adjusted means, it is possible to find an answer for this question .

In a single scientific study there is a high probability of appearance of differences among sample means, due to sampling hesitation. But in the long run the group means will have an equal value .

Adjusted means in ANCOVA

In an ANCOVA adjusted Y means are established by subtracting the part of the value form results that are related to or predictable from the covariates. Thanks to this solution it is possible to make a correction of any confound of the covariates or suppress some of the error variance and most importantly, increase the statistical power of conducted testes .

Examples of Adjusted mean

• Adjusted mean can be used to adjust the mean of a sample set by removing outliers or extreme values. For example, if a survey is conducted to determine the average age of people in a city, the adjusted mean can be used to adjust the mean after removing any outliers such as a person who is much older than the other respondents.
• Adjusted mean can also be used to measure the average performance of a team or group. For example, if a basketball team has five players with different levels of performance, the adjusted mean can be used to measure the average performance of the team after adjusting for individual performance.

Advantages of Adjusted mean

An adjusted mean is an important statistical measure used to determine the average of a dataset. It has a number of advantages, including:

• Increased accuracy: Adjusted means account for any outliers or skewed distributions in the data, providing a more accurate average than the unadjusted mean.
• Greater reliability: Adjusted means are usually more reliable than unadjusted means, because they are less affected by random variation or outliers in the data.
• Improved confidence: Adjusted means provide a more reliable average, making it easier to draw meaningful conclusions from the data.
• Aids in the comparison of datasets: Adjusted means can be used to compare data from different sources, and to make predictions about the likely outcomes in future data sets.

Limitations of Adjusted mean

• The adjusted mean has several limitations. First, it is based on linear regression, so it is not suitable for non-linear models. Second, it assumes that the data is normally distributed, which may not always be the case. Third, it relies on the assumption that all variables are independent, which may not be the case. Fourth, it ignores the presence of outliers, which can significantly affect the results. Finally, it assumes that all observations are equally important, which may not be the case when some observations are more influential than others.

Other approaches related to Adjusted mean

An adjusted mean is a statistical measure that is used to evaluate the performance of a sample set. Other approaches related to adjusted mean are:

• Weighted Average: This is a type of average that takes into account the relative importance of each element in the sample set, and then gives each element a corresponding weight based on its importance.
• Trimmed Mean: This is a type of average that excludes a certain number of elements at the beginning and end of the sample set in order to reduce the effect of outliers.
• Robust Mean: This is a type of mean that is designed to be more resistant to outliers and extreme values in the data set.

In summary, adjusted mean is a statistical measure commonly used to evaluate the performance of a sample set, and other approaches related to it include weighted average, trimmed mean, and robust mean.

Footnotes

Adjusted mean — recommended articles

Random error — Experimental error — Heteroskedasticity — Statistical power — Statistical significance — Cronbach Alpha — Mann-Whitney U test — Parametric analysis — Types of indicators — Legacy Planning

References

• Huitema B.E. (2011), The Analysis of Covariance and Alternatives: Statistical Methods for Experiments, Quasi-Experiments, and Single-Case Studies, John Wiley & Sons.
• Kramer C.Y. (1957), Extension of multiple range tests to group correlated adjusted means, Biometrics, 13(1).
• Lomax R.G., Hahs-Vaughn D.L. (2012), An Introduction to Statistical Concepts: Third Edition, Routledge.
• Warner R.M. (2013), Applied Statistics: From Bivariate Through Multivariate Techniques, SAGE Publications.

Author: Oksana Szłapowska