Graphical Evaluation and Review Technique

Graphical Evaluation and Review Technique (GERT) is one of the network charts. The method was created in early sixties and first described by Alan B. Pritsker in 1966. His publication remains the most popular and accessible description of GERT (see references for link). The main application of the method are poorly defined, highly probabilistic R&D projects, where there can be many alternative paths and loops.

GERT vs. other network diagrams

Its much less popular than PERT (Program Evaluation and Review Technique) or CPM (Critical Path Method). However it has can offer much more than those methods. PERT or CPM are very popular in most projects, but they have their limitations. The main are:

• there are no alternative paths - all activities have to be performed
• there are no loops - it is not possible to repeat activity, next similar activity has to be added
• there are no decisions in the diagram - no and, or, xor options which help to choose proper path
• there are no scaling - it is not possible to replace some detailed group of activities with the one summary task.

GERT doesn't have those limitations. But it comes at a cost of more sophisticated diagram.

General GERT rules

GERT uses activity-on-arrow notation only. That means that each activity is described on arrow. The nodes are used to connect activities, but also to determine type and conditions of relations between them.

Each task has two parameters: duration and probability of appearance.

There are three logical operators in GERT which concern activities incoming to the node:

• XOR - alternative (only one path possible)
• OR - alternative (one or more paths can be performed)
• AND - all paths have to be performed

The most common is AND, which means that every incoming activity has to happen before the outcoming one start.

There are also two types of relations that concern activities outcoming from the node:

• deterministic - every outcoming activity has probability equal to 1, which means that every one will be performed
• probabilistic - each outcoming activity has some probability of appearance.

Each node consists of one logical operator and one relation, which gives six combinations:

GERT example

In this example two space vehicles are being sent and meet in the space. The success of the mission is possible only if both are successfully launched.

Mission success has AND operator, as both vehicles are required. But mission failure has OR operator, as if at least one of them fails, the mission fails.

The example comes from A.A.B. Pritsker publication (see references).

Loops

The example below shows simple loop. The activity can be performed for the first time or (XOR) for the next time. Thus XOR in the beginning. If the result of the activity is not acceptable, the activity is repeated. The probability of repeating can be calculated.

Time and probability calculation

Calculation of duration requires analysis of probability and duration.

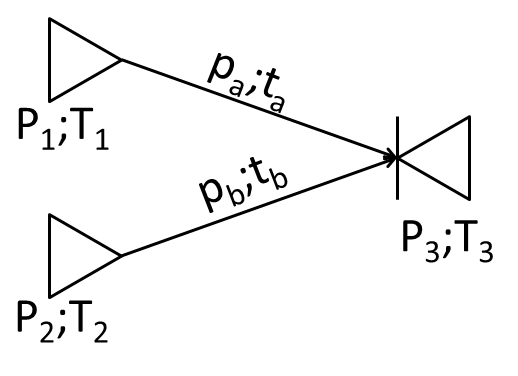
The equations below show how to calculate probability and duration of arriving at node 3 from nodes 1 and 2, which are alternative.

$P_{3}=P_{1}p_{a}+P_{2}p_{b}$

${\overline {T}}_{3}={\frac {P_{1}p_{a}({\overline {T}}_{1}+t_{a})+P_{2}p_{b}({\overline {T}}_{2}+t_{b})}{P_{1}p_{a}+P_{2}p_{b}}}$

Advantages of Graphical Evaluation and Review Technique

Graphical Evaluation and Review Technique (GERT) is a powerful network charting method that provides a visual overview of complex projects with multiple paths and dependencies. It has several advantages, including:

• Efficiency: GERT makes it easy to identify project tasks, dependencies, and alternative paths. This can help streamline project planning and ensure that all tasks are completed in the most efficient manner.
• Visibility: GERT charts provide a visual representation of the project, allowing team members to quickly identify potential issues and make critical decisions.
• Flexibility: GERT allows project managers to easily adjust project plans as needed, allowing projects to adapt to changing circumstances.
• Scalability: GERT is scalable, meaning it can be used to plan projects of any size or complexity.

Limitations of Graphical Evaluation and Review Technique

Graphical Evaluation and Review Technique (GERT) has several limitations. These include:

• GERT only works best with a small number of activities and tasks. As the number of activities increase, GERT becomes too complex and difficult to use.
• GERT does not take into account resource availability and constraints. It is possible to create a GERT chart that is not feasible to implement due to lack of resources or other restrictions.
• GERT is mostly used for R&D projects, and it is not suitable for projects with multiple objectives or goals.
• GERT does not account for delays and changes in the project. Therefore, it is not suitable for dynamic environments.
• GERT does not take into account the influence of external factors such as market conditions, regulations, or other external conditions.

Other approaches related to Graphical Evaluation and Review Technique

Graphical Evaluation and Review Technique (GERT) is one of the network charting techniques used to manage and analyze complex and probabilistic projects. There are various approaches that can be used to supplement GERT, such as:

• Critical Path Method (CPM): This method is used to identify the sequences of tasks that need to be completed in order to deliver a project. It focuses on the longest path of tasks and works towards ensuring that the path is completed in the shortest time possible.
• Program Evaluation and Review Technique (PERT): This is similar to CPM, but it allows for some flexibility in the tasks by introducing a probability factor to the tasks. It is used to plan and control the progress of a project while allowing for uncertainty.
• Monte Carlo Simulation: This approach uses random sampling to simulate multiple scenarios and analyze the probability of achieving a desired outcome. It is used to identify the most likely outcome of a project, given the probability of different paths and tasks.

In summary, GERT is a network charting technique that can be supplemented by other approaches such as Critical Path Method, Program Evaluation and Review Technique, and Monte Carlo Simulation, in order to manage and analyze complex and probabilistic projects.

Graphical Evaluation and Review Technique — recommended articles

Critical path method — Arrow diagram — Linear programming — MoSCoW technique — Project lifecycle — Subproject — Sprint backlog — Network charts — Quantitative risk analysis

References

• Pritsker, A. A. B. (April 1966). GERT: Graphical Evaluation and Review Technique. National Aeronautics and Space Administration under Contract No. NASr-21.
• Wolpaw, J. R., Birbaumer, N., McFarland, D. J., Pfurtscheller, G., & Vaughan, T. M. (2002). Brain-computer interfaces for communication and control. Clinical neurophysiology, 113(6), 767-791.
• Kurihara, K., & Nishiuchi, N. (2002). Efficient Monte Carlo simulation method of GERT-type network for project management. Computers & Industrial Engineering, 42(2), 521-531.